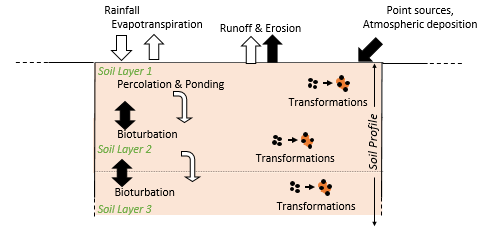
Soil Percolation in the NanoFASE Model
As a consequence of the vertical percolation of water through the given soil profile, ENMs may be buried deep in the soil, preventing them from being transferred to water bodies via soil erosion.
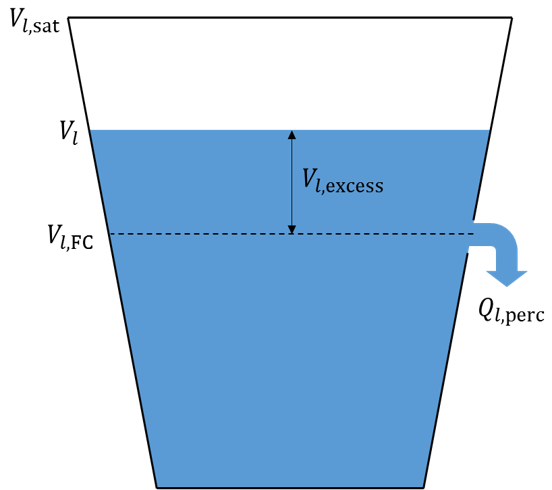1. Water percolation through each soil layer is calculated using a storage routing approach. Each layer has a field capacity, \(V_{l,FC}\) (m3 m-2). Percolation occurs only when the volume of water in the layer \(V_{l,> V_{l,FC}\). The amount exceeding this capacity is termed the "excess", \(V_{l,excess}\) :
\(If V_{l}> V_{l,FC}\rightarrow V_{l,excess}= min(V_{l}-V_{l,FC},V_{l,sat}-V_{l,FC})\)
\(If V_{l}\leq V_{l,FC}\rightarrow V_{l,excess}=0\)
2. The excess water \(V_{l,excess}\) percolates out of the bucket (layer) into the layer below, at a rate \(q_{l, perc}\) [m s-1]
\(q_{l, perc} = \frac{V_{l,excess}}{\delta t}(1-exp(-\frac{\delta t}{t_{perc}}))\)
where \(\delta t\) is the length of the model time step(s) and \(t_{perc}\) is the travel time for percolation. The latter is given by:
\(t_{perc}=\frac{V_{l,sat}-V_{l,FC}}{K_{sat}}\)
where \(V_{l,sat\) [m3 m-2] is the depth of water in the layer when completely saturated, and \(K_{sat}\) [m s-1] is the saturated hydraulic conductivity for the layer.
|
|
Used in |
Read more |
Read also |
|
Consult the NanoFASE Library to see abstracts of these deliverable reports: |
Neitsch, S. L., Arnold, J. G., Kiniry, J. R., & Williams, J. R. (2011). Soil and Water Assessment Tool - Theoretical Documentation: Texas Water Resources Institute Technical report 406, Texas A&M University System, College Station, Texas, U.S. |
Contact
Virginie Keller
Centre for Ecology and Hydrology (CEH)