Dry deposition calculation

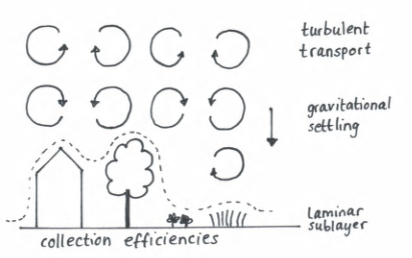
Dry deposition occurs through several pathways that occur partly in parallel. In analogy to resistances in electrical circuits, the resistance approach is used. For particles, the deposition velocity Vd is determined by the gravitational settling velocity (or sedimentation velocity Vs) and the inverse of the aerodynamic resistance Ra and the overall quasi-laminar resistance Rs.

\(V_{d}=\frac{1}{R_{a}+R_{s}+V_{s}R_{a}R_{s}} +V_{2}\)
Deposition velocity in resistance approach

\(R_{s}=\frac{1}{\epsilon _{0}u*(E_{B+}E_{IM}+E_{IN})R_{1}}\)

Surface resistance consisting of efficiencies for Brownian diffusion, impaction and interception

\(V_{3}=\frac{\rho D_{p}^{2}gC}{18\eta }\)
Gravitational settling velocity

The aerodynamic resistance is related to vertical turbulent fluxes and depends on the stability of the atmosphere.

The quasi-laminar resistance depends on the friction velocity \(u*\) (depending on wind speed and roughness) collection efficiencies from Brownian diffusion (\(E_{B}\)), the collection length for impaction (\(E_{IM}\)) and the collection length for interception (\(E_{IN}\)). These depend on surface properties like size of leaves and surface roughness, and particle size. R is the fraction of particles that sticks to the surface (rebound), there is no rebound when the surface is wet and \(R_{1}=1\) in that case.

Settling velocity depends on the particle density \(\rho\) and size \(D\), gravitational acceleration \(g\), slip correction coefficient \(C_{c}\) and viscosity of air \(\eta\).          

Execution

 

The algorithm by itself can be executed easily on a pocket calculator or spreadsheet but requires detailed input on underlying variables and parameters, such as surface roughness, wind speed, and atmospheric stability. It is beyond the scope of the present page to go into detail on all aspects of the calculation. For further detail we refer to the literature.

 Used in
 

 
              










                     Atmospheric dry deposition

Read more

Read also
 

NanoFASE uses parameterization based on Zhang et al (2001). Details are described in the LOTOS-EUROS documentation.

Seinfeld, J. H. and Pandis S. N.: Atmospheric Chemistry and Physics: from air pollution to climate, Wiley- Interscience, Hoboken, N.J., 2006​.

Zhang, L., Gong, S., Padro, J., and Barrie, L.: A size-segregated particle dry deposition scheme for an atmospheric aerosol module, Atmos. Environ., 39, 3291–3303, 2001.​

Petroff, A. and Zhang, L.: Development and validation of a size-resolved particle dry deposition scheme for application in aerosol transport models, Geosci. Model Dev., 3, 753-769, https://doi.org/10.5194/gmd-3-753-2010, 2010.

Contact

 

  Astrid Manders​

  TNO, Netherlands​