Particle diffusivity in air

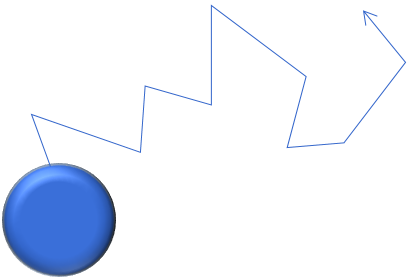
Airborne particles are in constant random Brownian motion, due to interaction with the surrounding gas molecules. Upon collision, a molecule transfers momentum to the particle, causing the particle to move. Due to the random nature of Brownian motion, the diffusional particle motion is also random and omnidirectional. Diffusional motion increases with decreasing particle size, whereas it is typically negligible for particles >100 nm. 

 

D= \frac{k\cdot T\cdot C_{C}}{3\pi \cdot \eta \cdot d_{p}}

(1) Particle diffusivity

 

C_{C}=1+\frac{2\cdot \lambda }{d_{p}}\left [ 1.165+0.483\cdot exp\left ( -\frac{0.997\cdot \lambda }{2\cdot d_{p}} \right ) \right ]

(2) Cunningham slip correction factor

 

 

x_{rms}=\sqrt{2\cdot D\cdot t}

(3) Root mean square displacement

The particle diffusivity D in equation (1) describes a particle’s ability to be moved by the collision with gas molecules. It increases with increasing temperature T and decreasing particle size dp.k is the Boltzmann constant, \etathe gas viscosity and CC the Cunningham slip correction factor, described in equation (2).


The Cunningham slip correction factor CC is needed to describe the particle size-dependent surface interaction between particles and molecules. In equation (2), \lambda is the mean free path of the gas molecules.


Due to the random nature of the particle diffusion, the direction of the motion and therefore the exact location of a particle after time t cannot be predicted. However, the root mean square displacement xrms, which describes how a particle may be displaced from its original location, can be estimated by equation (3).

Execution
 

These equations are purely deterministic and can easily be solved using a pocket calculator or spreadsheet software.                    

 

Used in
 

               

 
                       Coagulation                                                           Diffusion

Read more

Read also
 

 
W. Hinds (1999), Aerosol Technology – Properties, Behavior, and Measurement of Airborne Particles, John Wiley & Sons.
A. Einstein (1905),  Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen, Ann. Phys. 17: 549-560.

Contact

 

  Christof Asbach

  Institut für Energie- und Umwelttechnik (IUTA)

  Email: asbach@iuta.de